A thesis project by Reinier Joosse
Supervisors: Emiel Stoelinga, Leo van Neutegem
Process supervisor: Harry Nieboer
University supervisor: Nils Jansen
Second assessor: Daniel Strüber
Machine learning models are being deployed more and more in everyday life. This enables your car to recognize street signs on the side of the road. You can unlock your smartphone with just your face. And supermarkets recommend you new products based on your previous purchases.
As machine learning models are used more and more, we want to know about any potential security issues with these models and prevent them before they become a problem. It turns out that researchers found that machine learning models can be attacked using so-called adversarial attacks. These are very small modifications of the model's input such that a human does not see any difference, but it causes the model to make a completely incorrect decision.
This can cause security problems in the real world. For example, consider a "stop" sign on the side of the road. A hacker might add some small stickers to this sign such that you do not see any difference, while your car suddenly thinks it is a "highway" sign.
Fortunately, there are some ways to protect our models against such adversarial inputs. In particular, we can invent mechanisms that detect whether an input has been tampered with. Think of these defences like an email spam filter. A spam filter looks at all incoming emails and flags some of them as spam.
We will let the question of how we can design such an adversarial attack detector rest for now. There exist many designs for these detectors; some work well, others work less well. Rather, we are now interested in the question: exactly how well do these detectors work? We want the detectors to detect all attacks, yet we do not want them to raise any alarms about normal inputs. Analogously, we want our spam filter to delete all emails that are actually spam, but we want to keep all normal emails.
Of course, we could gather many attacks and test whether our defence mechanism detects them all. We could also gather many normal inputs and test whether our defence mechanism lets them all pass. But such test sets give us a false sense of security. It may well be that we trained our defence to detect all attacks that we already know of. But of course, a real hacker is not going to try attacks that we already know of. Instead, they will be creative and come up with new attacks to bypass our security.
All of this raises the following question:
To be able to answer the question above, we first had to ask ourselves the following:
It was first discovered by Szegedy et al. that adversarial attacks can be designed against neural networks, a commonly used machine learning model. These attacks do not only exist for models that recognize images, but also, for instance, for models that recognize spoken words in audio recordings. This was nicely exemplified by Schönherr et al.
A perturbation of an original input is only an adversarial attack if it is sufficiently close to the input that the attack is based on. For example, if an image of a "stop" sign is modified so heavily that it obviously no longer looks like a stop sign to a human, then it is not called an adversarial example. In short, an adversarial attack is a perturbation of an input for a machine learning model such that a human sees little to no difference, yet it causes the model to make a different decision.
Since we are particularly concerned with adversarial attack detectors for neural networks, it would be useful if we can formally prove properties of those neural networks. For instance, can we prove that no adversarial attack is possible for a particular neural network? Or can we prove that our detector detects all possible attacks?
Formal verification of neural networks has been studied in the past by other researchers. For example, Huang et al. found a way to perform a layer-by-layer analysis of a neural network to see if an adversarial example exists within a given distance of a normal input. Also, Katz et al. created a tool called "Reluplex" which can verify properties of neural networks, including robustness against adversarial examples. The latter tool was later extended and renamed to Marabou. These techniques are based on SMT solving.
In previous research, Carlini et al. measured the robustness of neural networks by using Reluplex to find the minimally distorted adversarial example. That is, given an original image, they measured the minimal amount by which it needs to be perturbed such that the result is an adversarial attack. The intuition behind this approach is that if the network is very robust against attacks, then finding an adversarial example will require greater perturbations to original inputs than for weaker networks. Our own solution to the problem is closely related to this approach.
We propose two metrics to estimate the quality of adversarial attack detectors:
Furthermore, they refer to the notions of false positives and false negatives. These concepts are similar to the concepts used in, for example, medical tests. If a medical test indicates that the patient has the disease, we say that the outcome is positive; otherwise, the outcome is negative. Unfortunately, medical tests are not always 100% accurate: sometimes the outcome is positive but the patient really does not have the disease (false positives); and sometimes the outcome is negative but the patient really does have the disease (false positives). Analogously, we say that an input to our neural network is a false positive if our detector flags it as adversarial, but the input is really not adversarial; and an input is a false negative if our detector thinks it is not adversarial, yet in reality it is.
Finally, we must define what we mean by the word "close". There are several methods available to measure the distance between inputs. For example, if our inputs are images, we could count the number of pixels that are different. Furthermore, we need to define a boundary and say: within this boundary of distance, we consider the inputs to be close, and outside the boundary, they are no longer close. Clearly, the choice we make here depends on the type of inputs we use and on how close a perturbation of an input must be to its original for us to still label it as an adversarial attack.
In summary, these metrics take a test set of normal images, and for each image they ask: is it possible to perturb this image — while staying within a certain distance bound (for some notion of "distance") — such that it becomes a false positive (or false negative)?
If it is possible to create such a false negative or false positive for most of the images in the test set, then that indicates that the detector is not very good. If, on the other hand, this is not possible for any of the tested images, then that indicates that the detector is good.
To compute the answer to these questions, we used the Marabou tool. We will not list the details of how this is achieved here, but we refer to the original thesis.
We proposed two new metrics that estimate the quality of adversarial attack detectors. The quality of detectors can also be estimated using a simple test set with both attacks and normal examples. When using a test set, however, we expected that we are not really measuring the detector's effectiveness against real-life adversarial attacks, but only its effectiveness against the old attacks in the test set. In short, we expect that we will get different (more reliable) results when using the two new metrics compared to when we test using a test set with attacks.
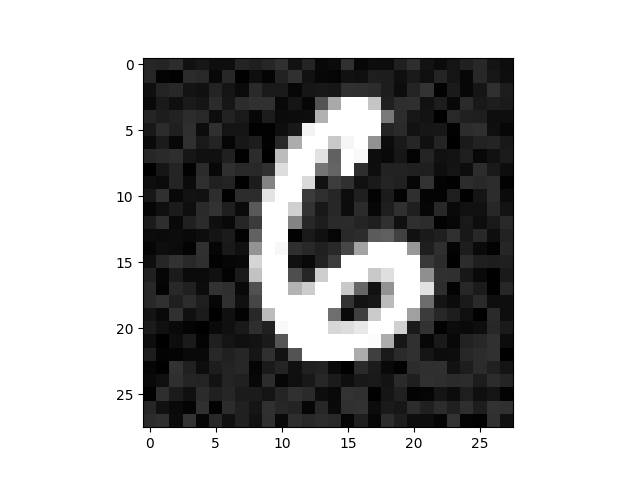
To see if this is indeed the case, we performed experiments with nine different detectors. These detectors were trained to detect attacks on a neural network that can recognize handwritten digits. Specifically, the neural network classifies images from the MNIST dataset. This dataset contains grayscale pictures of 28 by 28 pixels of handwritten digits. An adversarial attack on this network is an image that looks like one number (e.g. 6) that has been deliberately perturbed such that the network classifies it as a different number (e.g. 4). Therefore, the nine detectors take images of handwritten digits and judge whether such an image is an adversarial attack.
For each of these detectors, we evaluated its quality according to both a plain test set, and the two new metrics. The results are plotted in the graphs below, where each dot represents one detector. In these graphs, the quality according to the test set is shown on the X-axis, where the quality increases from right to left; and the quality according to the new metric is shown on the Y-axis, where the quality increases from top to bottom. The left graph shows the new metric related to the false negatives on the Y-axis, and the right graph shows the metric related to the false positives on the Y-axis.
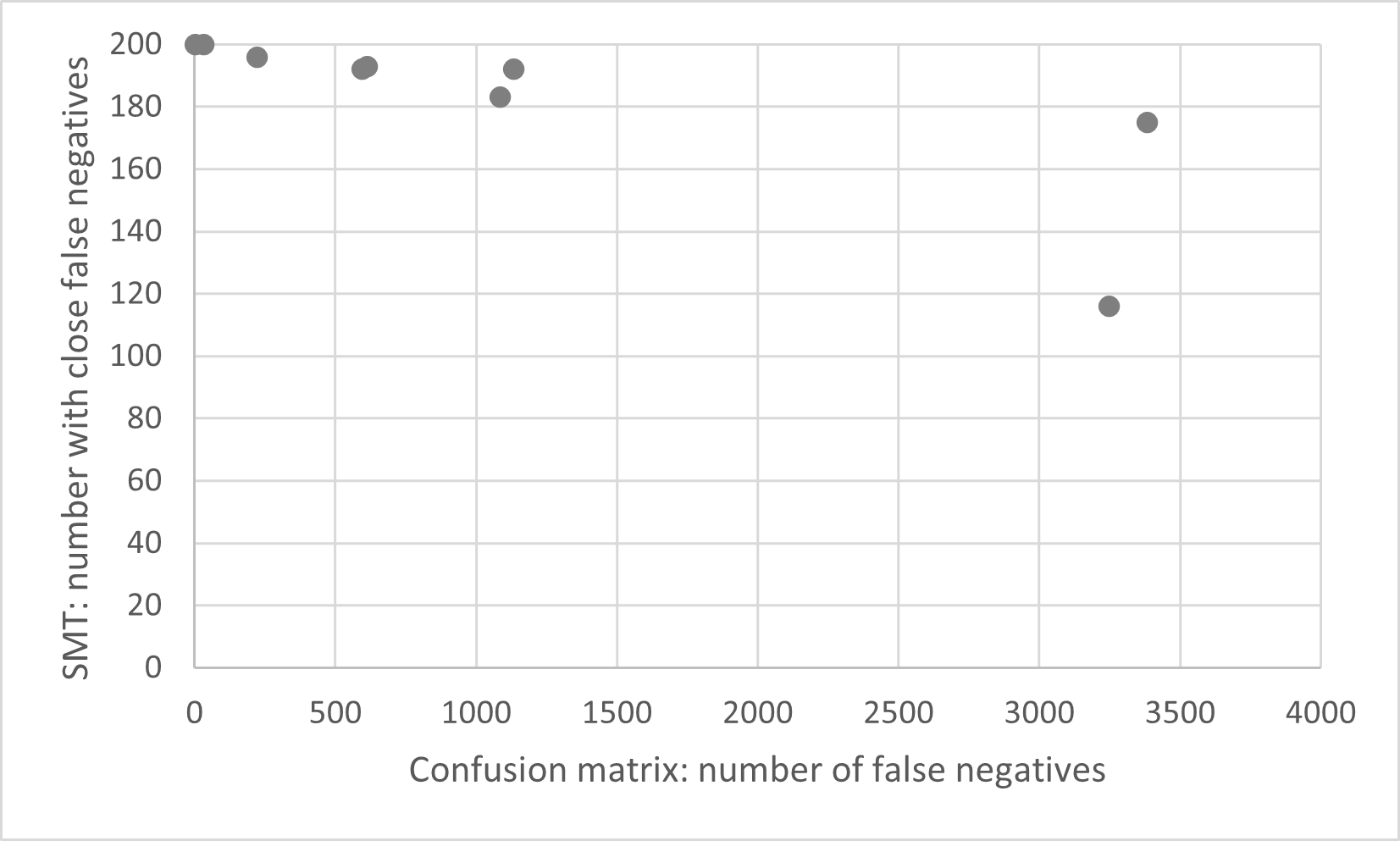
In the left graph, a negative correlation can be observed between the two metrics. This graph shows the quality with respect to the number of false negatives: that is, the number of images that are really adversarial, but not flagged as such by the detector. The negative correlation indicates that as the quality goes up according to the test set, the quality actually goes down according to our new metric. This is an interesting result. It suggests that the detector is overfitting on the attacks in the test set. Therefore, it is very good at detecting those old attacks. However, at the same time, the new metric shows that the detector is not really good at detecting attacks in general.
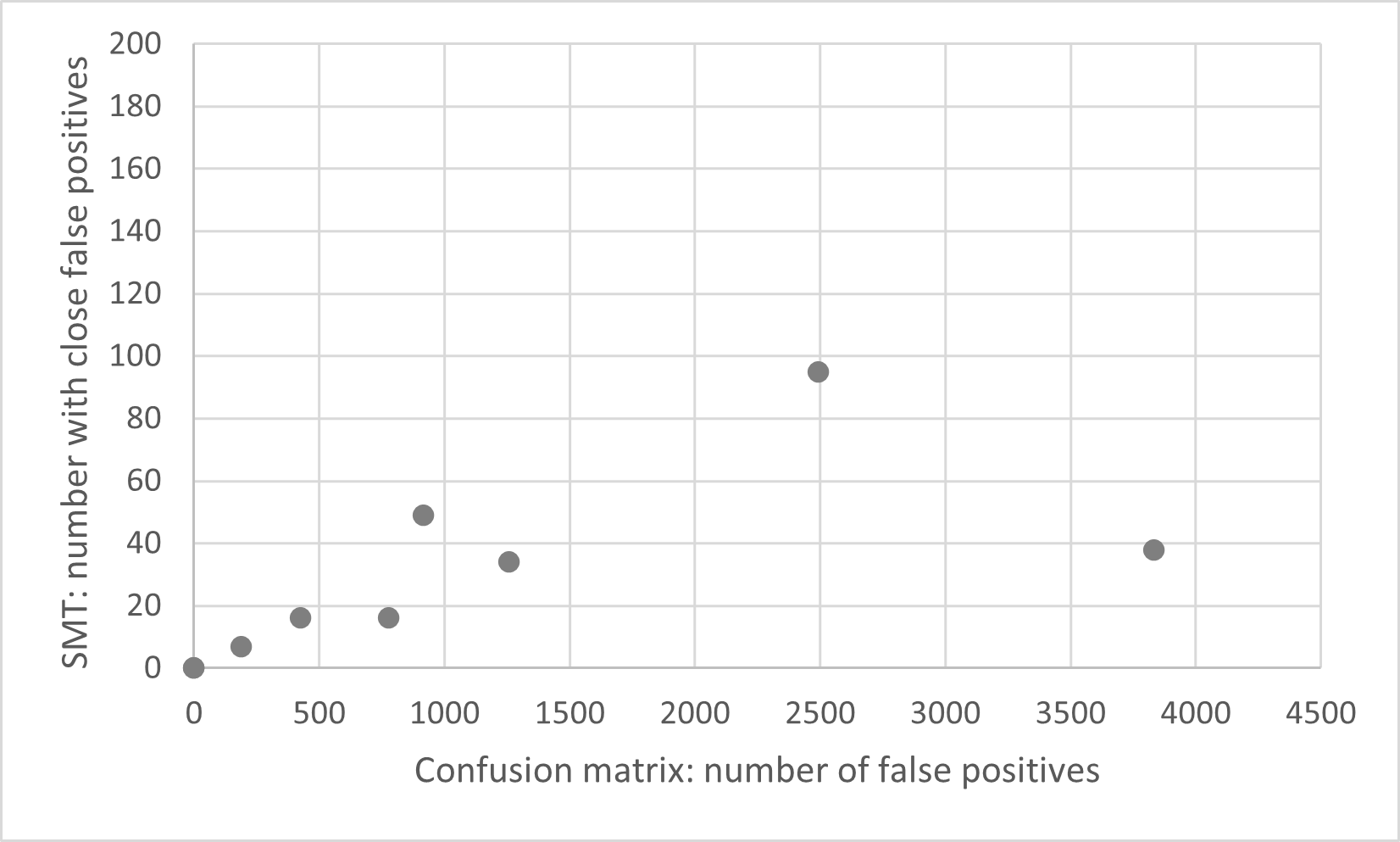
The graph on the right shows the quality with respect to the number of false negatives: that is, the number of images that are really not adversarial, yet the detector flags them as adversarial. This graph shows a positive correlation, which indicates that as the quality goes up according to the test set, it also goes up according to our new metric. This indicates that the detectors are not overfitting on normal examples.
We can conclude from these results that our two new metrics are indeed useful when we want to know the quality of adversarial attack detectors. While it costs a bit of time to answer the questions posed by the metrics, they do not suffer from the historic bias, which is problematic when we only test using a test set with old attacks.
There are multiple interesting directions for future research that builds upon this work. The following list provides a few examples.